Quels phénomènes principaux sont candidats pour expliquer ces améliorations ?
Surface d’échange nanoparticules-liquide
Prenons un exemple pour illustrer l’importance de cette surface de contact entre les nanoparticules et le liquide.
Exemple
Supposons que nos nanoparticules soient sphériques et d’un diamètre de 10 nm, chose que l’on sait tout à fait obtenir en pratique. Pour rendre le calcul possible, il faut supposer que la suspension soit homogène et que chaque nanoparticule soit régulièrement espacée de ses voisines. On choisit de les disposer suivant une maille cubique en découpant le volume de fluide en petits cubes de 25 nm de côté avec une nanoparticule au centre de ceux-ci (Figure 23). C’est très raisonnable puisque ça représente une fraction volumique de ~3,3 %.
Dans seulement 1 cm3 de ce nanofluide « parfait », on comptabilise donc 400 0003 nanoparticules sphériques, c’est-à-dire 6,4.1016 particules, soit 64 millions de milliards. Cela représente une surface de contact entre toutes les nanoparticules et le liquide de 20 m2 par centimètre cube de nanofluide, ce qui est considérable.
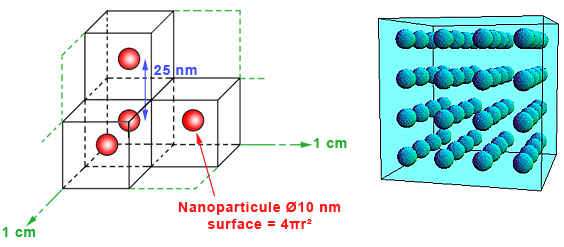 Fig. 23 : Répartition homogène et théorique de nanoparticules au sein d’un liquide
Fig. 23 : Répartition homogène et théorique de nanoparticules au sein d’un liquideSi l’on rapporte cet exemple à une unité de masse, sans tenir compte d’un arrangement quelconque des nanoparticules de 10 nm, la surface spécifique d’échange vaut environ 67 m2 par gramme de nanopoudre de cuivre ou encore 222 m2/g pour de la nanopoudre d’aluminium. En comparaison, un gramme de poudre de microparticules sphériques de cuivre de 0,01 mm de diamètre ne représente que quelques malheureux 670 cm2… La surface spécifique est inversement proportionnelle au rayon des nanoparticules.
Notons que la forme sphérique est la plus mauvaise, car c’est la forme géométrique qui présente le moins de surface externe pour un volume donné. Diverses études montrent que des nanoparticules ayant des facteurs de forme plus importants, comme des cylindriques ou des tubes, sont un peu plus efficaces que des sphères du fait d’un ratio surface/volume plus élevé, menant à plus d’atomes en contact avec le liquide de base. La surface spécifique de petits nanotubes de carbone se chiffre dans les 250 à 500 m2/g, c’est bien plus qu’avec des sphères.
On comprend l’intérêt d’avoir des particules de taille très réduite et en concentration suffisante pour faire exploser la valeur de la surface d’échange à l’intérieur du nanofluide. Ainsi, un plus grand pourcentage d’atomes constituant les nanoparticules peut interagir directement avec ceux du liquide environnant pour le transfert thermique. D’un point de vue théorique, un fluide est censé exprimer tout son potentiel avec une distribution homogène de petites nanoparticules. Des études confirment effectivement que la conductivité thermique augmente quand on diminue la taille moyenne des nanoparticules pour un même matériau. On attribue cette amélioration à l’augmentation de la surface de contact et au mouvement brownien, décrit ci-après, qui s’accentue. Toutefois, leur seule taille n’est pas non plus un critère suffisant pour prédire la qualité d’un nanofluide.
En effet, certaines expériences montrent aussi le contraire avec de meilleurs résultats pour de plus grosses nanoparticules. Il y a en fait un paramètre embêtant à contrôler, lié aux regroupements, qui intervient dans cette contradiction et que l’on désigne sous le terme « d’agrégation fractale ». Cette agglomération de particules en paquets est un frein à l’augmentation de la surface d’échange interne au fluide, mais elle peut aussi être bénéfique d’un autre point de vue. On peut l’expliquer par la formation de chemins directs que la chaleur va emprunter pour se répandre de nanoparticule en nanoparticule du fait de leur contact. Le transfert est bien plus rapide en passant par conduction dans ces structures à grande conductivité plutôt que par le liquide. Au final, cela donne une conductivité thermique effective plus élevée pour le nanofluide (Figure 24).
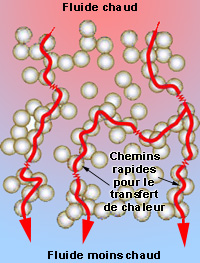 Fig. 24 : Les agrégats de nanoparticules créent des chemins préférentiels à haute conductivité thermique par rapport au liquide de base
Fig. 24 : Les agrégats de nanoparticules créent des chemins préférentiels à haute conductivité thermique par rapport au liquide de baseSi on combine ces chaînes de nanoparticules et le fait que la conduction en leur sein se fasse de manière plus ou moins balistique à cause de leur petite taille, on obtient une structure percolante qui transmet la chaleur d’un bout à l’autre de manière très efficace.
Le mouvement brownien et la microconvection
Le mouvement brownien des nanoparticules en suspension est la manifestation de leurs déplacements constants et aléatoires au sein du nanofluide. Ils sont causés par les incessantes collisions avec les molécules du liquide qui se déplacent dans toutes les directions sous l’effet de l’excitation thermique (la température du milieu est l’image de cette agitation). Les nanoparticules sont suffisamment petites pour être poussées par les chocs reçus et elles peuvent alors parcourir une certaine distance (très petite), avant de repartir dans une autre direction suite à de nouveaux chocs et ainsi de suite. Il en résulte un mouvement d’ensemble chaotique que l’on appelle le mouvement brownien (Figure 25).
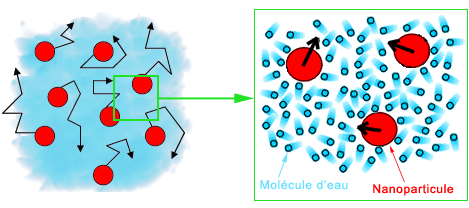 Fig. 25 : Agitation désordonnée de toutes les nanoparticules suite aux chocs avec les molécules de liquide
Fig. 25 : Agitation désordonnée de toutes les nanoparticules suite aux chocs avec les molécules de liquidePlus les nanoparticules seront grosses, plus ce mouvement brownien sera faible, car elles seront plus difficiles à bouger du fait d’une inertie plus importante et elles auront une vitesse de déplacement plus faible. Pour une nanoparticule composée d’un millier d’atomes de cuivre dans de l’eau maintenue à 25 °C, sa vitesse moyenne est de l’ordre de 1 m/s, alors qu’une grosse nanoparticule composée d’un milliard d’atomes aura plutôt une vitesse de l’ordre de 1 mm/s. Ce mouvement brownien a donc un intérêt tout particulier si les nanoparticules ont une taille suffisamment réduite. Il va empêcher celles-ci de sédimenter, car elles sont en perpétuel mouvement, y compris vers le haut, contre la gravité. Il faudrait alors attendre des mois ou des années pour que les nanoparticules retombent si le fluide est laissé dans un bocal statique, si un jour elles retombent…
On peut percevoir ce mouvement brownien en pratique en comparant ce qu’il se passe après le dépôt d’une petite goutte de colorant dans de l’eau seule et dans un nanofluide au repos (Figure 26). Il ne se passe presque rien dans l’eau faute de mouvement important, l’excitation thermique des molécules d’eau étant trop insignifiante pour une diffusion rapide. Par contre, dans le nanofluide, la goutte est clairement dispersée par les mouvements importants des nanoparticules qui opèrent un petit brassage localement. Ce microbrassage est une aide bienvenue et il se fait tout seul. On peut alors parler de microconvection, autrement dit du brassage à une échelle microscopique. C’est intéressant d’un point de vue thermique, car il va superposer son action à celle de la convection à plus grande échelle.
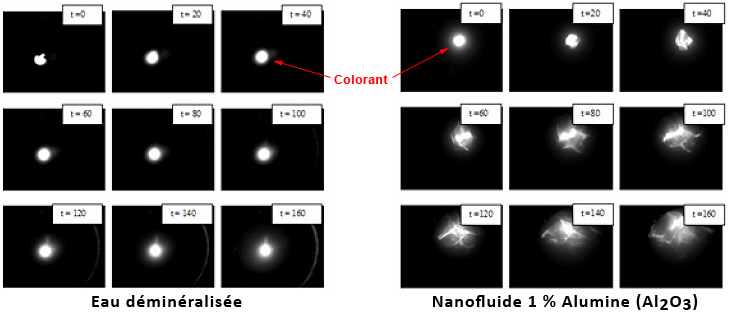 Fig. 26 : Dans le nanofluide, le colorant s’éparpille à cause du mouvement des nanoparticules. Dans l’eau pure, pas grand-chose…
Fig. 26 : Dans le nanofluide, le colorant s’éparpille à cause du mouvement des nanoparticules. Dans l’eau pure, pas grand-chose…Avec l’exemple de la goutte, on imagine aisément que si celle-ci est un volume de fluide chaud, sa chaleur va pouvoir être échangée et répartie plus efficacement au sein du liquide grâce à cette microconvection. Chaque nanoparticule absorbant une certaine énergie thermique va pouvoir la transporter rapidement en un autre lieu un peu plus éloigné pour échanger avec les molécules de liquide et ainsi rétablir l’équilibre thermique. L’inverse est aussi possible si la nanoparticule est plus froide que le liquide qui l’entoure, elle va alors absorber une partie de sa chaleur. Le nombre de collisions de molécules en un temps donné pour l’échange thermique est donc bien supérieur à celui de la convection normale.
Ce mouvement brownien rend aussi les nanofluides plus sensibles à la température que les fluides normaux. Plus la température est importante, plus l’agitation moléculaire est intense et plus les nanoparticules sont chahutées, améliorant d’autant plus la microconvection et donc la conductivité thermique du nanofluide (Figure 27).
Divers essais ont montré que cette conductivité pouvait grimper de 80 % si l’on travaillait avec un nanofluide comportant 0,5 % de nanotubes de carbone à 40 °C plutôt qu’à 25 °C. Bien sûr, on peut grimper encore plus haut en température pour l’améliorer, mais ça n’a rien d’intéressant pour un watercooling de PC d’avoir un fluide si chaud. Par contre, ça l’est bien plus pour des systèmes dissipant beaucoup d’énergie et ayant des températures de fonctionnement élevées comme dans le cas d’une voiture, même si une saturation de la hausse de conductivité thermique peut apparaitre. Dans le cas d’une voiture ou d’un camion, cela permettrait de réduire la taille du radiateur principal par exemple avec tous les avantages que cela comporte.
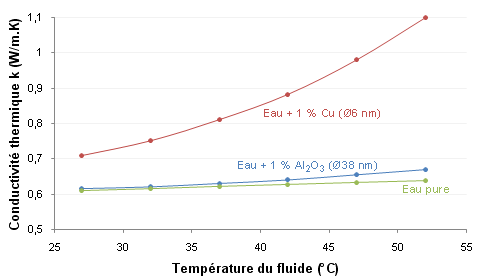 Fig. 27 : Amélioration de la conductivité thermique avec la température, les petites nanoparticules en profitant plus
Fig. 27 : Amélioration de la conductivité thermique avec la température, les petites nanoparticules en profitant plusCette sensibilité accrue à la température peut aussi avoir un intérêt particulier, le nanofluide pouvant devenir « intelligent ». Si un système présente des zones localisées à fortes densités de flux thermique, ces zones seront plus chaudes et donc le nanofluide qui arrivera dessus va voir sa conductivité thermique s’améliorer spontanément, ce qui conduit à une meilleure efficacité dans une région qui en a besoin. On pourrait aussi se poser la question inverse sur l’intérêt d’un nanofluide dans des systèmes utilisant des fluides de refroidissement à basse température, car leur potentiel diminuant avec cette température, ils se révéleront être probablement peu intéressants dans ce domaine d’utilisation.
L’action du mouvement brownien est supposée être l’une des principales raisons pour expliquer l’amélioration « anormale » de la conductivité thermique d’un nanofluide. Néanmoins, cela peut avoir un inconvénient sur la qualité à long terme, car il induit plus de chocs interparticulaires et donc potentiellement plus de formation d’agrégats si on ne fait pas ce qu’il faut pour les éviter…
Le petit frère du mouvement brownien, le principe de thermophorèse
La thermophorèse, un autre phénomène convectif lié au mouvement brownien, peut rentrer en ligne de compte, même si son influence est limitée dans des applications à faible différentiel de température, comme c’est le cas avec un watercooling de PC en général. Son intérêt se situe au voisinage d’une paroi chauffée ou dans des régions à fort gradient de température.
Au voisinage d’une nanoparticule, cette action de thermophorèse engendre l’apparition d’une force dans une direction préférentielle, qui résulte du déséquilibre des chocs avec les molécules du liquide. Près d’une paroi dissipant une certaine quantité chaleur, le fluide est naturellement plus chaud, donc les molécules de liquide sont plus excitées thermiquement avec pour conséquence d’avoir une plus grande vitesse que celles présentes du côté froid (Figure 28). Les nanoparticules sont donc poussées plus fortement par les molécules du côté chaud à cause de la différence de quantité de mouvement. Cela les emmène automatiquement vers les régions plus froides, favorisant une fois de plus l’homogénéisation de température.
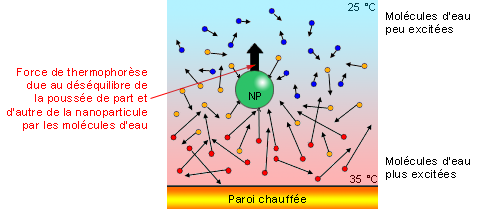 Fig. 28 : Action de la thermophorèse sur une nanoparticule
Fig. 28 : Action de la thermophorèse sur une nanoparticulePhonons balistiques pour transporter la chaleur
La nature du transport de la chaleur au sein des nanoparticules est l’un des effets conductifs qui pourraient avoir son rôle dans l’amélioration observée. En effet, la conduction thermique se retrouve largement influencée par les effets de taille. Dans des structures ayant des dimensions supérieures à quelques centaines de nanomètres, le transport de la chaleur est gouverné par un mécanisme dit « diffusif » que l’on peut modéliser avec l’équation de la chaleur de Fourier, mais celle-ci n’est plus valide aux très petites échelles de longueur et de temps. Pour les nanostructures, des approches stochastiques plus complexes deviennent nécessaires pour décrire la situation avec l’équation de transport de Boltzmann par exemple.
Avant de décrire le régime balistique, rappelons ce qu’est la conduction à un niveau atomique et le concept des phonons (oui, avec un N).
Quel est le vecteur de transport de l’énergie thermique dans un solide ? Si d’un point de vue extérieur, la conduction de chaleur semble être issue d’un phénomène unique, ce n’est en réalité pas le cas suivant le matériau étudié. Dans les solides, la chaleur est principalement transférée par conduction dans tout le réseau atomique par deux mécanismes :
- la transmission des vibrations d’atomes
- le déplacement des électrons libres
Dans un solide cristallin, les atomes sont rangés de manière ordonnée suivant une géométrie définie et ils sont liés les uns aux autres par les forces d’interaction (liaison covalente par exemple). Ces forces ne sont pas des liens infiniment rigides, il subsiste une souplesse de mouvement pour les particules. Les atomes peuvent osciller légèrement autour de leur position d’équilibre selon leur degré d’excitation thermique. Plus on leur communique d’énergie, plus ils vont s’agiter (amplitude de vibration plus grande) et plus la température sera élevée localement.
D’un point de vue schématique, on peut représenter cet assemblage d’atomes comme un ensemble masses-ressorts où les atomes sont les masses et les forces sont les ressorts (Figure 29). Il est facile de comprendre que si on écarte l’une des masses de sa position d’équilibre et qu’on la relâche, elle va se mettre à osciller du fait du rappel des forces élastiques auxquelles elle est soumise. Elle perturbera le reste du réseau et tout finira par vibrer, car tout est lié. En situation, cet écartement est équivalent à apporter une quantité d’énergie à un atome pour augmenter son niveau d’excitation.
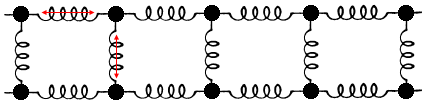 Fig. 29 : Schématisation d’un ensemble d’atomes (masses) liés par les forces interatomiques (ressorts) à l’équilibre
Fig. 29 : Schématisation d’un ensemble d’atomes (masses) liés par les forces interatomiques (ressorts) à l’équilibreL’amplitude du déplacement d’un atome autour de sa position moyenne, loin de la température de fusion du matériau, est extrêmement faible. Elle est de l’ordre de quelques centièmes de la distance entre deux atomes voisins, soit quelques picomètres (10-12 m) et s’opère à grande fréquence, au-delà du térahertz (1012 à 1014 Hz). La vibration produite se propage à tout l’ensemble en raison des liaisons interatomiques, chaque particule transmettant son mouvement vibratoire particulier a ses voisines, on parle de vibration cristalline. Les atomes perturbés vont céder une partie de leur énergie cinétique aux atomes environnants en les entrainant avec eux dans leurs mouvements afin de rétablir l’équilibre général. L’énergie thermique se déplace ainsi de proche en proche dans le cristal (Figure 30).
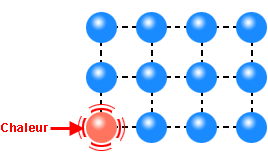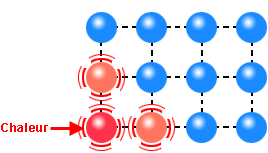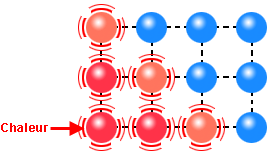
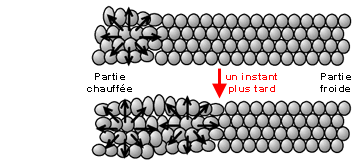 Fig. 30 : Conduction de la chaleur de proche en proche grâce à la transmission des vibrations d’atomes dans un solide cristallin
Fig. 30 : Conduction de la chaleur de proche en proche grâce à la transmission des vibrations d’atomes dans un solide cristallinOn peut évoquer deux exemples simples de mise en vibration suite à une sollicitation où les atomes vibrent à la même fréquence (Figures 31 et 32). Dans un cas réel, la direction des multiples sollicitations est aléatoire par rapport à l’alignement des atomes dans le réseau et leur allure dépend de la fréquence d’excitation, ce qui complique sérieusement l’allure des oscillations. Néanmoins, on pourra les décomposer en mouvements élémentaires, ce qui va nous amener à la notion de phonon.
 Fig. 31 : Exemple de sollicitation longitudinale dans un cristal 1D
Fig. 31 : Exemple de sollicitation longitudinale dans un cristal 1D Fig. 32 : Exemple de sollicitation transversale dans un cristal 1D
Fig. 32 : Exemple de sollicitation transversale dans un cristal 1DLes vibrations induites par une perturbation de nature thermique sont à voir comme la propagation d’ondes de déformation qui vont exciter successivement tout ce qui se trouve sur leur chemin en se déplaçant à la vitesse du son dans le solide considéré. Cette vitesse de transmission, pour les grandes longueurs d’onde, est de l’ordre de plusieurs kilomètres par seconde dans les métaux. Par exemple, elle est de 3,9 km/s dans le cuivre (onde longitudinale) ou encore de 20 km/s dans le diamant grâce à son réseau rigide qui lui confère son étonnante conductivité thermique.
L’arrangement périodique des atomes dans un cristal va induire des mouvements d’ensemble coordonnés. Tous ces mouvements peuvent être décomposés en une superposition de vibrations élémentaires qu’on appelle les « modes propres » et qui se font à des fréquences bien déterminées, les « fréquences propres ». Un mode normal de vibration est un mode dans lequel chaque élément d’un réseau vibre à la même fréquence (comme les deux animations ci-dessus). L’analogie la plus simple est celle de la corde de guitare que l’on pince et qui vibre ensuite à sa fréquence propre pour produire une note donnée. A chacun de ces modes propres (en nombre fini dans un solide), on va y associer un phonon et plus précisément un phonon acoustique (il existe aussi le phonon optique plus complexe…). Les phonons sont importants, car ils sont responsables des aspects comme la conductivité thermique et électrique, la chaleur spécifique, la supraconductivité, la propagation des ondes sonores…
La mécanique quantique énonce que l’énergie de ces vibrations élémentaires est quantifiée : elle ne peut augmenter que par addition de paquets d’énergie. Un phonon est cette quantité d’énergie élémentaire qui caractérise un mode propre de vibration. Les ondes de déformation contiendront par conséquent de 1 à N phonons, qu’elles soient créées par l’agitation thermique ou par une sollicitation extérieure. Le phonon est aux ondes acoustiques ce que le photon est aux ondes lumineuses, d’où la ressemblance de leur nom. On dit que le phonon est un quantum d’énergie de vibration (plus petite quantité d’énergie que peut posséder un mode de vibration cristalline), tout comme le photon est un quantum d’énergie lumineuse (plus petite unité d’énergie que peut posséder un mode de vibration lumineuse).
Avec la notion de dualité onde-corpuscule de la mécanique quantique et bien qu’un phonon soit une entité immatérielle de nature ondulatoire/vibratoire, on peut le considérer comme une quasi-particule, c’est-à-dire une particule virtuelle. Cela simplifie la compréhension, car celle-ci est vue et décrite comme le porteur d’une certaine quantité d’énergie à distribuer à travers le réseau et capable d’établir des collisions. Un corps cristallin échange donc des phonons lorsqu’il gagne ou perd de l’énergie. Quand il y a un déséquilibre de température dans le solide, le transfert thermique s’opère de la région chaude où il y a beaucoup de phonons (beaucoup d’agitation dans tous les sens) vers la région froide où leur densité est moindre.
Dans le cas des nanoparticules, on peut parler de transport balistique pour qualifier la très faible probabilité qu’un électron ou qu’un phonon subisse des collisions durant son trajet, car la distance à parcourir est statistiquement trop faible pour que ça arrive. Dit simplement, il n’y a pas de résistance à l’avancée de l’énergie. Cela se produit quand toutes les dimensions caractéristiques (longueur, diamètre…) de l’objet sont inférieures au « libre parcours moyen ». Ce terme désigne la distance parcourue par un porteur d’énergie entre deux événements de diffusion, c’est-à-dire entre deux collisions avec des impuretés (atomes d’une autre nature), des défauts de structure atomique ou d’autres porteurs. Ce libre parcours moyen varie en général de 5 nm à 200-300 nm à température ambiante suivant le matériau, donc en plein dans le domaine d’échelle des nanoparticules.
Au contraire, en régime diffusif, les porteurs subissent des collisions qui modifient leur trajectoire et qui peuvent induire, ou non, un transfert d’une partie de leur énergie cinétique à des atomes ou des porteurs. C’est grâce aux innombrables collisions que l’équilibre thermique se réalise (Figure 33).
 Fig. 33 : Différence entre un transport d’énergie diffusif et balistique suivant les dimensions de l’objet
Fig. 33 : Différence entre un transport d’énergie diffusif et balistique suivant les dimensions de l’objetPlus il y a de collisions, plus l’avancée de l’énergie au sein du solide est ralentie et plus un matériau a une faible conductivité thermique. Plus on s’éloigne de la source chaude et moins on a d’énergie à échanger, les atomes lointains sont donc moins excités. Il se forme alors une grande différence de température entre la partie chauffée et celle refroidie, ce qui n’est pas intéressant du point de vue des performances thermiques. La contribution des phonons est plus importante dans une structure atomique ordonnée et pure plutôt que dans une structure amorphe et/ou impure, car ils pourront s’y propager bien mieux et amener l’énergie loin du point d’origine sans trop en distribuer en cours de route. C’est ce qui explique que le diamant dispose d’une conductivité thermique élevée du fait d’un réseau rigide très pur et très ordonné, alors que du simple verre dispose d’une conductivité thermique ridicule vu sa structure atomique complètement aléatoire.
Le transport balistique est intéressant, car le gradient de température entre la partie chaude et la partie froide n’est pas défini. Dans un morceau de matière suffisamment petit, il n’y a pas de collisions internes pour rétablir l’équilibre thermique, c’est une situation assez particulière (Figure 34). La nanoparticule offre alors une température identique à sa surface pour restaurer l’équilibre thermique avec le liquide. Même si ce n’est pas le cas, c’est un peu comme si le matériau devenait idéal et que la conductivité avait une valeur infinie à l’intérieur, mais il ne faut pas oublier de tenir compte des effets avec la surface (résistance de Kapitza introduisant des discontinuités de température).
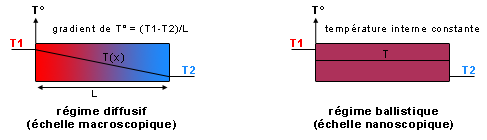 Fig. 34 : Dans un milieu homogène et isotrope, un gradient de température linéaire se développe en diffusif contrairement au balistique
Fig. 34 : Dans un milieu homogène et isotrope, un gradient de température linéaire se développe en diffusif contrairement au balistiqueCertaines hypothèses envisagent aussi que si un phonon issu d’une nanoparticule peut persister dans le liquide, sur une distance ultra courte vu le manque d’ordre, et être transmis directement à une autre nanoparticule, cela conduirait à une meilleure efficacité du transport d’énergie. Sachant que le mouvement brownien génère un nombre gigantesque de rapprochements et de collisions de nanoparticules, pourquoi pas…
Couche interfaciale nanoparticule-liquide
De récentes études suggèrent qu’un phénomène de surface pourrait avoir un rôle dans l’amélioration de la conductivité thermique. Il est reconnu qu’à l’interface entre un liquide et une surface solide, il se forme une couche de liquide qui, contrairement aux molécules libres de ce liquide (qui se lient et se délient ~1011 fois par seconde entre elles plus précisément), a tendance à s’organiser en couches atomiques plus ou moins ordonnées. On pourrait le qualifier d’état intermédiaire entre un solide et un liquide pour imager. Une nanoparticule se voit alors entièremen







