Résistance thermique
Pour qualifier l’importance des facteurs qui agissent sur les performances de l’échangeur, il faut pouvoir décomposer leurs influences respectives en analysant ce qu’on appelle les résistance thermiques. Chacun d’entre eux pourra alors être quantifiés et comparés pour avoir une vision des points à améliorer.
Définissons tout d’abord ce qu’est une résistance thermique. C’est un critère de mesure de l’efficacité d’un système de refroidissement, indépendant des éléments extérieurs (radiateur, pompe..). On qualifie donc la performance du bloc seul et non pas d’un système tout entier, qui est en général unique. Cette résistance thermique doit être combinée avec les pertes de charges pour pouvoir déterminer le meilleur échangeur à un débit donné. Elle varie suivant le débit : plus ça débite, plus elle est petite, et inversement. On l’exprime en °C/W et plus elle est faible, mieux c’est évidemment. Par exemple, si l’on dit que tel waterblock a une résistance thermique de 0.1 °C/W (= augmentation de 0.1 °C par watt dissipé) à 300 L/h, cela signifie que pour un processeur dissipant 100 W et un débit volumique de 300 L/h d’eau qui rentre dans le bloc à 25 °C, la température de la base en contact avec le core sera égale à 25 + 0.1 * 100 = 35 °C. Il faut ajouter à cela la hausse de température due à la pâte thermique (~5 à 10 °C pour 100 W) pour avoir la température moyenne du core. Attention, cette hausse de température dépend de la surface du core donc du CPU ! Plus la surface de contact est étendue plus le décalage de température est faible.
On va détailler l’ensemble des résistances thermiques qui interviennent en fonction de la géométrie pour mieux comprendre le concept. Que ce soit un waterblock classique ou à microcanaux, la résistance thermique globale est la somme d’autres résistances thermiques qui sont toujours les mêmes, à savoir :
- résistance de la base dite résistance de conduction (loi de Fourier)
- résistance des ailettes également de conduction
- résistance de convection entre la paroi et le fluide
- résistance calorifique désignant le réchauffement du fluide entre l’entrée et la sortie
On va prendre pour exemple l’échangeur ci-dessous, soumis à un flux de chaleur homogène sur toute la surface de sa base avec de l’eau comme fluide caloporteur :
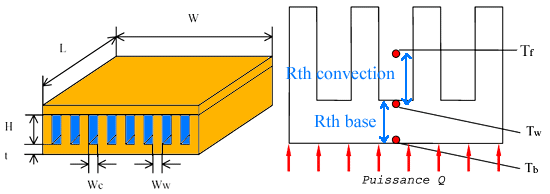
La résistance de la base exprime le fait que lorsque la chaleur traverse une quantité de matière, il y a une différence de température entre la face sur laquelle est appliqué le flux de chaleur (Tb) et la face que l’on souhaite refroidir (Tw). Elle dépend de l’aire de la surface, de l’épaisseur et de la conductivité thermique du matériau. Plus la base est épaisse, plus la résistante de conduction est élevée, et plus la différence de température Tb – Tw augmente. Cela nous empêche de faire tendre Tb vers Tw et il subsistera toujours le même écart quel que soit le refroidissement employé. Par exemple, si la paroi Tw est à 35 °C et la différence de température qu’occasionne la base vaut 5 °C pour 100 W (= 0.05 °C/W), la surface en contact avec le core sera à 40 °C. Une base épaisse est très utile dans certains cas pour étaler la puissance, mais complètement défavorable dans d’autres car elle va engendrer une augmentation de la température du core. Son épaisseur optimale est unique pour chaque design suivant la forme de l’écoulement dans l’échangeur. Dans le cas des microcanaux, la base est de très faible épaisseur en général, juste assez pour assurer la rigidité de l’ensemble. On va donc la choisir comme étant constante et négligeable devant le reste (= 0.0015 °C/W pour une base 40x40x1 mm en cuivre).
La résistance des ailettes sera également négligée pour les mêmes raisons que précédemment, car elles sont très fines et pas très hautes.
La résistance de convection est due au fait que la température des parois mouillées est différente de la température du fluide, à cause de la couche limite qui agit comme un film isolant, ça se passe entre Tw et Tf. Elle diminue si h augmente donc si la taille des canaux diminue. Elle diminue également si la surface mouillée augmente. Elle est donc inversement proportionnelle au produit de h et S et elle vaut 1/(h * S).
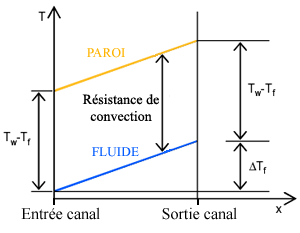 La résistance calorifique caractérise le réchauffement du fluide entre l’entrée et la sortie de l’échangeur, à cause de la puissance qu’il absorbe. Elle va donc dépendre exclusivement du débit, qui sera conditionné par la pompe choisie et la taille des canaux. Pour une puissance donnée et si le débit est faible, on aura un petit volume par unité de temps à réchauffer donc sa température sera plus élevée que si on passe le double de volume dans le même temps. Elle se traduit par une augmentation, notée Delta Tf, plus ou moins régulière de la température du fluide tout le long du canal. Le fluide qui se réchauffe oblige les ailettes à suivre son évolution de température car on ne peut pas être plus froid que le fluide lui-même, ça parait évident ! Le principe est explicité sur le schéma ci-contre et sur une image extraite d’une simulation numérique pour un écoulement laminaire qui passe entre 2 ailettes chauffées (vue de haut en coupe) :
La résistance calorifique caractérise le réchauffement du fluide entre l’entrée et la sortie de l’échangeur, à cause de la puissance qu’il absorbe. Elle va donc dépendre exclusivement du débit, qui sera conditionné par la pompe choisie et la taille des canaux. Pour une puissance donnée et si le débit est faible, on aura un petit volume par unité de temps à réchauffer donc sa température sera plus élevée que si on passe le double de volume dans le même temps. Elle se traduit par une augmentation, notée Delta Tf, plus ou moins régulière de la température du fluide tout le long du canal. Le fluide qui se réchauffe oblige les ailettes à suivre son évolution de température car on ne peut pas être plus froid que le fluide lui-même, ça parait évident ! Le principe est explicité sur le schéma ci-contre et sur une image extraite d’une simulation numérique pour un écoulement laminaire qui passe entre 2 ailettes chauffées (vue de haut en coupe) :

Le graphe ci-dessous montre la valeur de l’augmentation de température du fluide lorsqu’il passe dans un échangeur quelconque, soumis à une certaine puissance thermique, autrement dit c’est la résistance calorifique Delta Tf. C’est une comparaison entre les résultats obtenus à partir de mesures très précises que m’a fourni Bill Adams (testeur américain travaillant pour Swiftech) et mon calcul de thermodynamique pour apprécier l’excellente concordance des résultats :
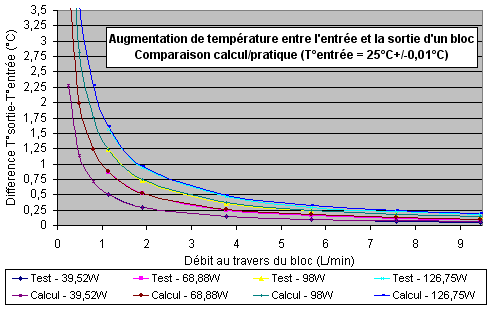
Avec ce graphe, on commence à percevoir l’un des rares inconvénients qui existent pour les microcanaux. Ceux qui ont par exemple un circuit comprenant un Atotech MC1 savent que le débit global est très faible, à cause de la très importante perte de charge du waterblock. Avec une pompe EHEIM 1046 (300 L/h maxi et 1.2 mCE maxi), 2 m de tuyau 6/8 et un radiateur, le débit qui passe dans l’Atotech est d’environ 850 mL/min soit 51 L/h. Avec les mêmes composants, le débit est d’environ 1.2 L/min soit 72 L/h avec un waterblock 1A-HV. Le débit est faible mais ils n’en sont pas moins très performants ! On comprend ici l’intérêt des tuyaux de petits diamètres pour une intégration propre, puisque l’on n’a pas beaucoup de débit à faire passer. En regardant le graphe du dessus, on se rends compte que le fluide va prendre ~2.3 °C en passant à travers l’Atotech pour une puissance réelle de 130 W alors qu’il ne prendrait que ~0.4 °C pour un Maze4 par exemple qui permettrait un débit nettement supérieur.
Cette différence de température va avoir pour conséquence de faire grimper la température des parois et donc du bloc tout entier, ce qui peut, si l’on réduit vraiment trop le débit, donner au final un mauvais waterblock. On gagne énormément sur la résistance de convection en diminuant la taille des canaux mais on perd de plus en plus sur le plan de la résistance calorifique. Il y a donc un compromis à trouver pour atteindre le minimum de la résistance thermique globale en ayant les canaux les plus fins possibles, tout en garantissant un débit suffisant.
Ayant connaissance de chacune des résistances en jeu, on peut définir la résistance thermique globale de l’échangeur, notée Rth globale, en les additionnant tout simplement. La Rth globale est désignée par une formule assez connue :
Rth globale = (Température base – Température fluide entrant) / Puissance dissipée
Attention, comme dit précédemment, on ne tient pas compte de la pâte thermique ici qui n’a rien à voir avec l’échangeur, on ne fait que qualifier le waterblock seul donc on prend la température de la base et non celle du processeur. On trace donc la courbe Rth convection + Rth calorifique (+ Rth conduction si on était pointilleux) en traduisant schématiquement tout ce que l’on vient de dire. On obtient une courbe d’allure parabolique présentant un minimum qui correspond à la plus faible Rth globale possible pour une certaine largeur de canal et c’est là qu’on a les meilleures performances :







