Elements de conception pour waterblocks – Page 5

Pour en revenir à nos résistances on a ici la démonstration des principes physiques pour comprendre comment se répartissent les températures dans une base. La mise en place d’ailettes et la façon dont le fluide parcourt le bloc vont influencer fortement Rs, il devient impossible de traiter cela de tête.

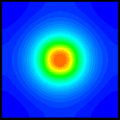
Prenons une plaque 50×50 mm dont on fait varier uniquement l’épaisseur, le core de 10×10 mm dissipant toujours la même puissance et le h sur le dessus étant constant. L’épaisseur variant, la répartition des températures va changer dans cette plaque ainsi que sur la face supérieure puisque l’on impose un h constant et non pas une température constante, ce qui est totalement différent. Ci-contre, la répartition des températures sur la face en contact avec le core, elle est de type concentrique autour de celui-ci.

L’échelle des températures est identique cette fois-ci pour chaque cas, on peut ainsi aisément comparer. Le h est faible (1000 W/m2·K) sur le dessus pour bien voir comment une « grosse » base améliore la température du core. Ca n’est pas vrai dans tous les cas on le verra par la suite avec des h importants créés par des techniques d’impact de jet par exemple. Voici 4 bases d’épaisseur différente vues en coupe au milieu avec leur répartition thermique :

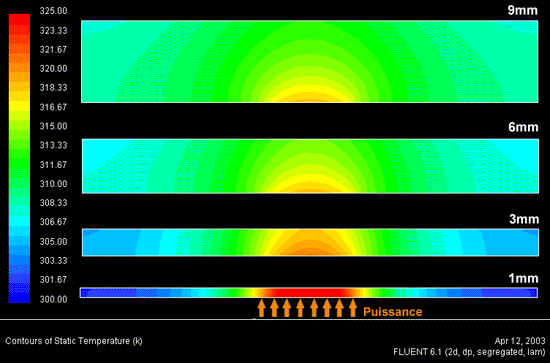
Le core avec la base de 1 mm est le plus chaud car cette base étant trop fine pour étaler la chaleur et le h étant trop faible pour l’absorber efficacement juste au dessus du core, il en résulte une augmentation de température dans la base ce qui fait grimper évidemment la température du core. N’oublions pas que la température du core est conditionnée par la température juste au dessus de lui donc de la pâte thermique, qui elle-même dépend de ce qui se trouve au dessus (contact base) et ainsi de suite… L’augmentation de l’épaisseur permet donc d’étaler la chaleur pour que le h créé n’ai pas trop de difficultés à absorber celle-ci en évitant la formation d’un point chaud au dessus du core. Voici les courbes de températures relevées sur le dessus de la plaque (toujours en coupe) :

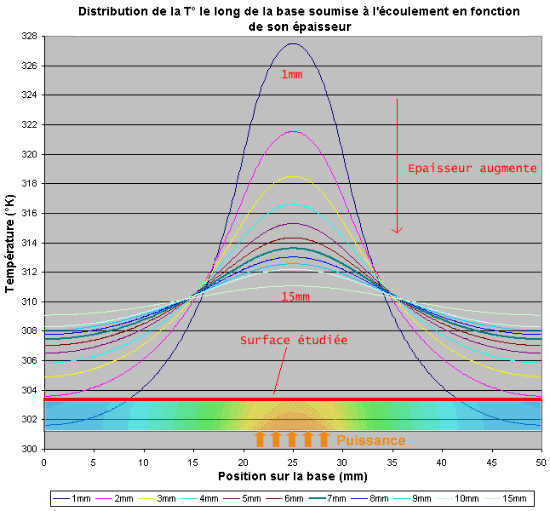
On retrouve bien un pic de chaleur au centre quand l’épaisseur est faible et une répartition de plus en plus homogène au fur et à mesure que l’épaisseur augmente. L’homogénéisation des températures sera bénéfique pour des blocs à écoulement « basique ». Le pic de chaleur sera exploité plus tard par des écoulements « puissants » car un autre point sur l’épaisseur de la base est à introduire avant de passer aux choses sérieuses.

On a vu au dessus que plus la base est épaisse plus sa Rf est élevée. Maintenant on va voir l’influence de Rf+Rs avec les différences de tailles qui existent entre les cores et la base. On prend une plaque de 50×50 mm dont on fait varier l’épaisseur et un core de 10×10 mm dissipant 70 W. On choisit un segment d’étude qui passe par le centre du core jusqu’au centre de la face supérieure de la plaque, avec Tc la température en bas et Tp en haut :

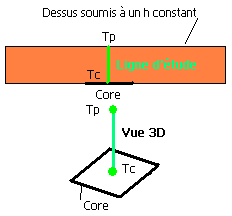
Cette différence de température Tc – Tp est reportée sur le graphe ci-dessous. Plusieurs valeurs de h sont testées pour montrer que quelque soit la « puissance » du refroidissement au dessus il existera toujours une différence de température entre la paroi supérieure et le core. Cette différence sera d’autant plus grande que la base sera épaisse. En réalité les écarts seront plus faibles puisqu’on se situe sur une surface (le core) et non pas sur un point (Tc), j’ai pris le point le plus chaud du core et du dessus de la plaque pour montrer simplement le phénomène :

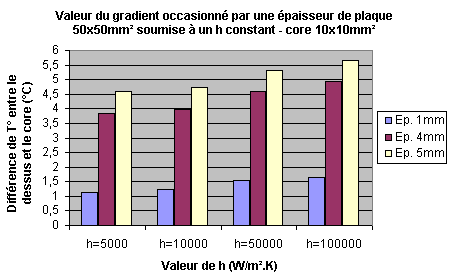
Pour une base de 5 mm par exemple, la différence Tc-Tp atteint 4.5 °C (la résistance de convection est incluse implicitement) et ceci quelque soit la force de h. Admettons que cet écart soit identique pour toute la surface du core, cela signifie que si l’eau au dessus est à 30 °C, la température du core sera au minimum absolu de 34.5 °C. Il faudrait de plus ajouter la hausse de température due à la pâte thermique non prise en compte ici. Attention, plus h augmente, plus Tc et Tp diminuent tout en gardant un certain écart à peu près constant. Cela peut donc paraître idiot d’augmenter l’épaisseur de la base mais il n’en ai rien car si vous la réduisez vous allez augmenter fortement Rs et donc risquer de faire pire que mieux. Pour illustrer encore ceci d’une manière différente, on trace la limite de température atteignable pour le contact base/core en fonction de l’intensité de h :

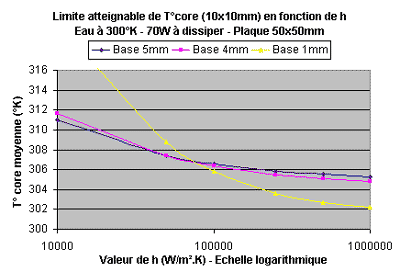
Toujours pour une simple plaque soumis à un h constant, on observe que pour des h petits les bases épaisses sont mieux pour étaler la chaleur sur toute la face supérieure. Au bout d’un moment le h devient assez important (écoulement « puissant ») pour que l’on puisse transférer efficacement la chaleur à l’eau sans avoir recours à une base épaisse. Si l’on continue à faire croître le h, on va tendre vers la résistance de Fourier Rf seule puisque la résistance de surface Rs, dépendant de h, va devenir assez petite. Les bases épaisses ayant une Rf plus grande que les bases fines, il est logique qu’elles soient moins bonnes. On ne pourra jamais atteindre une température égale à celle de l’eau car, quel que soit l’écoulement, la plaque induira toujours une résistance au passage de la chaleur. Les h au dessus de 70000-100000 W/m2.K sont inatteignables dans nos systèmes sans changement de phases et sans jets d’eau très rapides nécessitant une forte pression pour les créer.

Tout est donc dépendant du design que l’on a choisi et que l’on est capable d’usiner, c’est toujours une histoire de compromis qui s’installe. Il est évident que le meilleur bloc sera celui avec une base de faible épaisseur mais uniquement s’il utilise un écoulement « puissant » du type impact de jet ou qu’il possède une surface énorme (microcanaux) au dessus du core, sinon le résultat sera mauvais.

Résumé :

• Plus la base a une surface importante plus Rf diminue par contre Rs augmente si on garde le même h au dessus.
• L’épaisseur de base optimale dépend du design et du débit, elle est unique pour chaque débit. On voit donc une des difficultés qui apparaît lorsqu’il s’agit de faire un bloc destiné à être vendu car tout le monde n’utilise pas la même pompe. Il faut privilégier certaines plages de débits qui dépendront des pertes de charges du bloc.
• Moins on traverse de métal au dessus du core et plus le core pourra descendre en température (+ d’overclocking en général) en se rapprochant de la température de l’eau à condition que l’écoulement soit adapté et « puissant ».
• En étant très rapide en jugement, car chaque bloc est à considérer au cas par cas, on peut dire que les blocs ayant un écoulement « basique » nécessiteront une base plus grosse pour être au top car le h généré est assez faible en général. Contrairement aux blocs à impact de jet qui pourront avoir des bases plus fines grâce à un h beaucoup plus élevé.