Résistance de la base
La deuxième chose que la puissance rencontre est la base du waterblock. Cette partie nous intéresse beaucoup, car elle conditionne aussi une partie des performances qu’on obtiendra par la suite. Cette base sera paramétrée par sa longueur, sa largeur et son épaisseur. L’épaisseur à choisir est l’objet de beaucoup d’interrogations lors de la conception d’un waterblock home-made. On entend souvent dire qu’il faut la plus petite épaisseur possible pour que la chaleur arrive le plus vite dans l’eau, cette phrase peut être vraie, mais également fausse puisqu’elle est conditionnée par la géométrie du maze et la nature de l’écoulement. Il est difficile de dissocier la résistance de la base et la résistance de convection due à l’écoulement car les 2 sont liées par le coefficient h à la paroi et la géométrie du bloc. On va d’abord prendre les 2 séparément puis on y inclura la convection plus tard pour voir son influence. Ici on ne tient pas compte de la pâte thermique dans les points qu’on va traiter ci-après, quand je parlerais de température du core il s’agira de la température moyenne au contact supposé parfait du core et de la base. La pâte n’a aucune utilité pour l’étude du bloc en lui-même, c’est juste un décalage de température au final…
On prend 2 bases identiques : l’une soumise à une puissance uniformément répartie sur toute la face inférieure et l’autre soumise à une puissance localisée avec une différence de taille entre le core et la base (ce qui arrive en réalité).
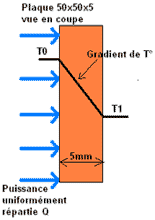 On sait, d’après la loi de conduction de Fourier, que la traversée d’une épaisseur de matériau entraîne une résistance thermique et donc un gradient de température le long de cette épaisseur. Autrement dit, la température varie d’une certaine manière suivant l’endroit où l’on se trouve dans l’épaisseur de la plaque. Dans le cas de gauche, la température décroît linéairement suivant l’épaisseur (matériau isotrope). On peut comprendre le phénomène en imaginant des tranches infiniment fines posées les unes sur les autres, chacune ayant sa propre température. La plus chaude sera celle où l’on applique la puissance et la plus froide à l’opposé comme sur le schéma ci-contre (T0 > T1).
On sait, d’après la loi de conduction de Fourier, que la traversée d’une épaisseur de matériau entraîne une résistance thermique et donc un gradient de température le long de cette épaisseur. Autrement dit, la température varie d’une certaine manière suivant l’endroit où l’on se trouve dans l’épaisseur de la plaque. Dans le cas de gauche, la température décroît linéairement suivant l’épaisseur (matériau isotrope). On peut comprendre le phénomène en imaginant des tranches infiniment fines posées les unes sur les autres, chacune ayant sa propre température. La plus chaude sera celle où l’on applique la puissance et la plus froide à l’opposé comme sur le schéma ci-contre (T0 > T1).
L’expression de cette résistance appelée Rf vaut Rf = L/(k.A) avec L l’épaisseur de la plaque (5 mm), k la conductivité thermique du matériau (400 W/m.K pour du cuivre) et A la surface d’application de la puissance (50 * 50 mm). Toujours dans le cas de gauche, on a Rf= 0.005/(400*0.052) = 0.005 °C/W. Cette valeur signifie que l’on aura une différence de température de part et d’autre de la plaque de 0.5 °C si l’on applique 100 W de puissance.
Si on arrive à avoir une température T1 de 20 °C par exemple, la face où la puissance s’applique sera à 20.5 °C. Il y aura toujours, quelque soit le moyen de refroidissement, une différence de 0.5 °C dans le cas d’une puissance uniformément répartie. On commence à percevoir un des aspects pénalisants de l’épaisseur de la base car il y aura toujours un décalage entre la température du fond du maze (différente de celle de l’eau) et celle du core. On va maintenant tracer Rf pour plusieurs plaques de 3 surfaces différentes pour montrer que Rf peut être réduite :
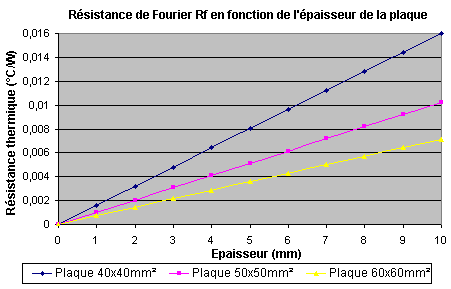
On observe que plus la plaque a une surface importante plus sa résistance de Fourier Rf diminue (voir formule du dessus). Il faut donc si possible utiliser une base de bloc la plus grande possible pour la minimiser. Entre une plaque de 40×40 mm et 60×60 mm d’épaisseur 6 mm on a une différence de résistance de ~0.006 °C/W, ce qui représente pour 100 W qui traverse cette plaque uniformément une température supérieure de 0.6 °C pour la plaque de 50 * 50 mm. Ca peut paraître ridicule mais cette résistance n’est pas la seule à rentrer en ligne de compte dans le calcul de la résistance totale de la base donc autant tout faire pour minimiser tout ce que l’on peut.
Cette résistance de Fourier existe toujours mais une autre apparaît en supplément lorsque la taille des 2 plaques en contact, le core et le bloc, sont de surfaces différentes. On l’appelle la résistance de surface notée Rs : elle reflète le fait que la chaleur ne se déplace plus seulement dans le sens de l’épaisseur mais aussi en largeur (puissance localisée) à cause des différences de tailles des 2 zones en contact. Cette résistance va dépendre du ratio géométrique des surfaces en contact, de l’épaisseur de la base ainsi que des échanges thermiques dans le bloc. L’expression physique de cette résistance est compliquée et n’a pas d’intérêt ici. Il faut juste savoir que plus la base a une grande surface et une épaisseur conséquente (inférieure quand même à 10mm au delà on y perds) plus Rs diminue.
Voici une visualisation du phénomène d’étalement en coupe : une plaque de 50x50x5 mm soumise à une même puissance dissipée par 5 cores différent allant de 50 mm à 10 mm de coté (passage d’uniforme à localisé) avec un coefficient h imposé sur le dessus de la plaque pour simuler une absorption de chaleur « générique » qui n’a pas d’importance ici :
La résistance thermique globale de notre base, appelée Rb, n’est donc plus à présent égale à Rf mais à Rb = Rf + Rs. On a vu que, suivant le ratio géométrique des 2 surfaces en contact, la résistance de surface varie, donc à design égal, plus le core est grand plus Rs va diminuer avec Rs = 0 quand on est en répartition uniforme. Tout ceci diminue Rb et augmente par conséquent les performances du bloc. Voici une plaque 50×50 mm soumise à un h constant sur le dessus, une même puissance dissipée par chaque core (sans IHS) et on ne fait varier que l’épaisseur de la plaque :
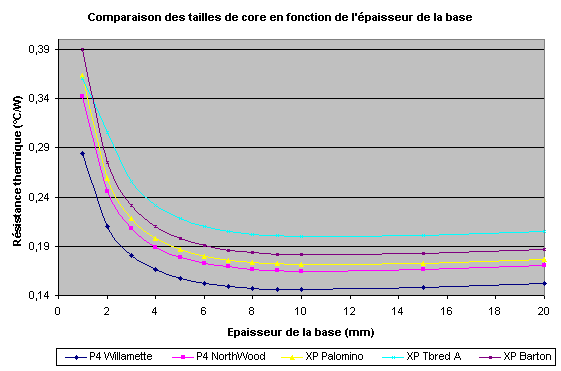
On observe que les cores les plus grands donnent les Rb les plus faibles donc les meilleures performances. L’épaisseur optimale se trouve, suivant les tailles des cores, entre 9 et 10 mm. Au delà Rs ne diminue quasiment plus car on est étalé presque au maximum et Rf, qui ne cesse de croître de façon linéaire avec l’épaisseur, prends le dessus donc la somme des 2 remonte à nouveau. Il existe donc un compromis unique à trouver qui assurera la résistance de base la plus faible qu’on puisse avoir. On le voit sur ce schéma :
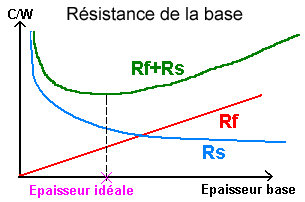
 Plus le core est grand plus la base peut être réduite en épaisseur pour atteindre les performances optimales. Attention, ces graphes sont valables pour une plaque simple de 50×50 mm soumise à un h constant. Imaginez un écoulement d’eau très simple sur le dessus sans impact et sans canaux cela donnerait un h à peu près constant. On peut faire une parenthèse sur l’explication à l’utilisation des plaques froides en ayant vu la résistance de la plaque et en assimilant la surface de la plaque froide comme délivrant un h constant…
Plus le core est grand plus la base peut être réduite en épaisseur pour atteindre les performances optimales. Attention, ces graphes sont valables pour une plaque simple de 50×50 mm soumise à un h constant. Imaginez un écoulement d’eau très simple sur le dessus sans impact et sans canaux cela donnerait un h à peu près constant. On peut faire une parenthèse sur l’explication à l’utilisation des plaques froides en ayant vu la résistance de la plaque et en assimilant la surface de la plaque froide comme délivrant un h constant…
Celles-ci servent de tampon thermique en évitant les écarts de température brutaux mais surtout elles permettent d’optimiser l’efficacité du Peltier en répartissant la chaleur sur toute sa surface de manière la plus équitable possible pour avoir la résistance thermique la plus faible. Ca n’est pas pour rien que Swiftech par exemple (image ci-contre) utilise des plaques froides de fortes épaisseurs (10 mm) en cuivre car ce sont celles qui donneront les meilleures performances. Les soi-disant plaques froides d’épaisseur de 3mm vendues dans le commerce sont trop fines pour avoir une efficacité maximale.







