Etudes de cas et optimisation
On va voir 2 exemples d’optimisation dans les 2 grandes classes de waterblocks qu’on peut distinguer : les écoulements « basiques » et les écoulements par impact, à savoir mon ancien maze en forme de spirale à angles droits et un Swiftech modifié.
Commençons par mon ancien bloc de 50x50x15 mm avec un maze spirale très simple à faire avec une fraiseuse manuelle. Sa base initiale prévue était de 5 mm, mais une erreur de manipulation a ramené la base à 3.5 mm. Voici le bloc en question :
 L’étude numérique réalisée s’est faite sous Fluent avec 20 cas 3D à traiter, à savoir 5 épaisseurs de base allant de 2 mm à 6 mm et 4 débits différents (68, 114, 227 et 340 L/h). Les embouts font 8 mm de diamètre interne, la zone de contact processeur fait 10×10 mm, la hauteur du maze fait 10 mm et le dessus en plexi n’intervient pas. A droite, le maillage initial utilisé sans raffinage au début.
L’étude numérique réalisée s’est faite sous Fluent avec 20 cas 3D à traiter, à savoir 5 épaisseurs de base allant de 2 mm à 6 mm et 4 débits différents (68, 114, 227 et 340 L/h). Les embouts font 8 mm de diamètre interne, la zone de contact processeur fait 10×10 mm, la hauteur du maze fait 10 mm et le dessus en plexi n’intervient pas. A droite, le maillage initial utilisé sans raffinage au début.
Le fluide est de l’eau qui rentre à 25 °C par l’embout central et le bloc est en cuivre. La puissance à dissiper est de 70 W sur 100 mm2. La température que j’appelle température du core est la moyenne des températures sur la surface de contact. On calcule ici un écoulement moyen car l’écoulement est instationnaire, c’est à dire qu’il varie autour de cet écoulement moyen suivant les tourbillons formés dans le flux. On va regarder l’allure du coefficient de convection h sur la paroi du fond du maze uniquement à 2 débits différents pour voir que h augmente avec le débit :
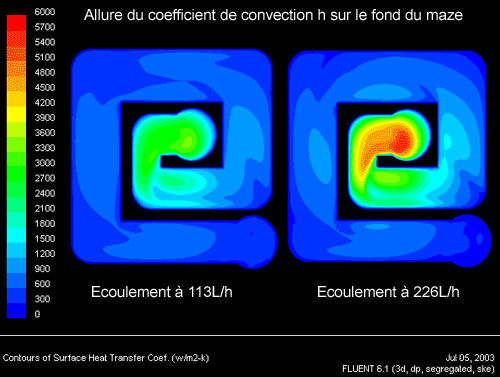
L’échelle de couleurs est la même pour les 2 débits pour pouvoir comparer aisément. Le h le plus élevé se situe naturellement sous la petite zone d’impact du jet entrant et dans la zone près de la première arête. Le h n’est pas très élevé puisque le jet impactant est assez gros (8 mm) et n’a donc pas une vitesse très élevé (1.25 m/s pour 226 L/h). Il diminue assez rapidement au fur et à mesure qu’on s’éloigne du centre car le flux d’eau devient presque parallèle aux parois mais h augmente très légèrement dans les zones où le fluide décolle (derrière chaque virage à 90°) car c’est un peu plus turbulent.
L’intérêt de ramener l’eau par le centre n’est pas trop du au fait que l’eau soit « froide », puisque la variation entre l’entrée et la sortie vaut ici 0.27 °C pour les 70 W réels absorbés à 227 L/h, mais c’est le fait que l’écoulement génère un grand h grâce à l’impact du jet là où on est le plus chaud. En arrivant par l’extérieur, on change la forme de l’écoulement mais la température du core ne varie que peu. Elle augmente un peu car on perd le bénéfice de l’impact au centre comme on le voit sur le graphe du dessous (même échelle). En inversant les 2 tuyaux dans mon système sans toucher au bloc, les différences de T° dans les mêmes conditions étaient imperceptibles, ça dissipe un peu moins de 70 W et j’ai un débit légèrement supérieur qui réduisent l’écart. Voici l’allure de h en arrivant de l’extérieur :
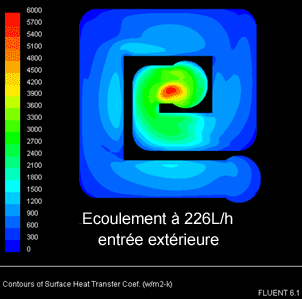
Voici à présent l’allure de la répartition des températures sur la paroi du fond du maze, elle est bien différente de la température de l’eau ! Plus on débite plus le bloc est froid puisque h augmente, notamment grâce à l’impact central plus puissant, et absorbe donc plus efficacement la chaleur de la paroi (même échelle) :
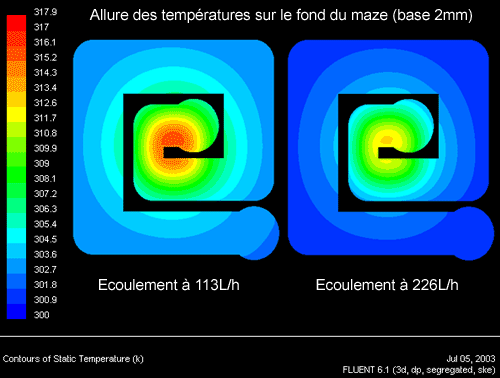
On rassemble tous les cas de figures calculés sur un même graphique pour apprécier le gain apporté par une base plus épaisse et d’un débit plus soutenu dans le cas présent. On remarquera que l’on tend vers une limite de température pour une base de 6 mm à 340 L/h, rien ne sert vraiment d’aller plus loin dans l’épaisseur car la courbe remontera ensuite. Augmenter à 7 mm par exemple ne fera qu’augmenter le poids du bloc pour un gain négligeable. Un débit encore plus élevé améliorerait les choses tout en permettant de réduire la base puisque le jet devenant puissant on a un moins grand besoin d’étaler la chaleur. Voici le relevé des résistances thermiques globales du bloc en fonction de la base et du débit, plus la Rth est faible mieux c’est :
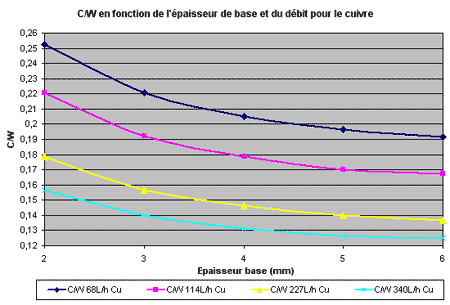
Plus la base est grosse moins on gagne à augmenter le débit, il suffit de regarder l’écart entre les débits extrêmes. Voici ci-dessous les même données mais affichées différemment pour avoir la température moyenne du core (au contact) en fonction du débit et de l’épaisseur. On retrouve la limite de température entre la base de 5 et 6mm car les 2 courbes sont très proches l’une de l’autre. La base atteint presque son épaisseur optimale pour minimiser sa résistance et aussi la résistance de convection en facilitant l’enlèvement de la chaleur par l’eau grâce à des parois « plus froides » et plus homogènes en température :
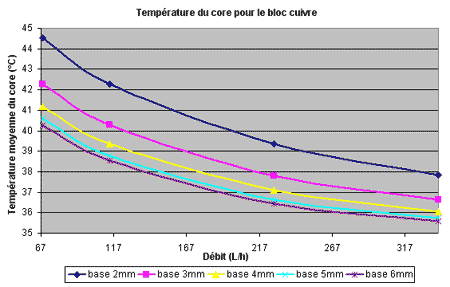
Une grosse base permet d’avoir des performances très correctes sans avoir besoin d’un débit élevé. Par exemple un bloc de base 6 mm à 117 L/h serait aussi bon qu’un bloc de base 2 mm à 290 L/h, tout ceci grâce à l’étalement de la chaleur sur tout le bloc ! Exactement comme sur un radiateur ventilé classique où une grosse base permet d’étaler la chaleur sur toutes les ailettes pour permettre au flux d’air, pas très « puissant » thermiquement parlant, de pouvoir extraire cette chaleur facilement. Et enfin on pourrait piqueter la surface au centre du bloc là où le jet s’écrase pour augmenter les performance comme dans le bloc qui suit.







