Méthode de mesure et de comparaison
Elle est basée sur une méthode calorimétrique qui énonce le fait que l’énergie perdue par l’eau, entre l’entrée et la sortie du radiateur, est intégralement dissipée par celui-ci. Rien de plus logique en somme, l’énergie ne disparaît pas par magie.
C’est d’ailleurs comme cela qu’on arrive à l’équilibre thermique dans un circuit classique. Au bout d’un certain temps sous une charge donnée, la température de l’eau ne varie plus, car le radiateur dissipe autant que ce qu’il reçoit du processeur (on suppose le circuit isolé pour négliger les pertes par les tuyaux, le PCB, etc.). On peut l’exprimer aussi de la manière suivante : l’élévation de température de l’eau à son passage dans le waterblock chauffé est exactement compensée par la descente de température lors du passage dans le radiateur. L’équilibre thermique peut alors prendre cette forme :
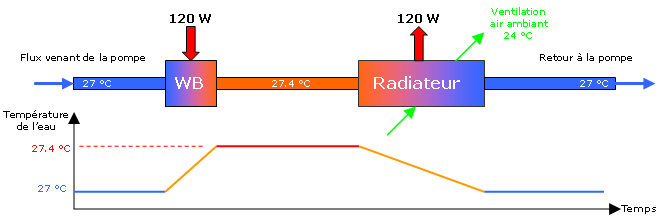
Pour un débit d’eau et une puissance à dissiper donnés, on aura toujours le même écart de température entre l’entrée et la sortie du radiateur quel que soit le modèle utilisé. On peut mettre plus d’ailettes ou ventiler comme un fou, l’écart sera toujours de 0.4 °C dans notre exemple précédent. Ce qui changera par contre, c’est la température de l’eau qui circule. Elle passera de 27 à 26 °C si l’on ventile plus par exemple (26.4 °C en entrée de radiateur et 26 °C en sortie).
Voici un autre exemple entre 2 radiateurs d’efficacité différente et soumis aux mêmes conditions extérieures :
Plus un radiateur est efficace, plus il est capable de maintenir un écart eau-air faible face à une grosse injection de puissance.
Détails de la mesure
On connaît parfaitement les propriétés physiques de l’eau entre 0 et 100 °C et notamment ici tout ce qui concerne sa capacité thermique massique notée Cp. Ce paramètre définit la quantité d’énergie (en joules) qu’un certain volume d’eau est capable d’emmagasiner pour une élévation unitaire de température. Cette valeur est connue puisqu’elle vaut 4186 J/kg·K à 20 °C. C’est à dire que pour élever 1 kilogramme d’eau de 20 à 21 °C, il faut lui fournir 4186 joules, c’est beaucoup. Il suffit alors de mesurer avec une grande précision la température à l’entrée et à la sortie du radiateur, puis connaissant le débit d’eau et la capacité thermique massique, on peut facilement remonter à la puissance exactement dissipée par ce radiateur.
On injecte donc à l’entrée de l’eau à 10 °C au dessus de l’air qui ventile le radiateur et l’on calcule ce qu’elle a perdu comme énergie en mesurant sa température en sortie. Une notion de temps est apporté par le débit massique (masse d’eau qui passe par seconde dans le radiateur), or une énergie rapportée sur un temps c’est une puissance en watt.
Suivant la géométrie du radiateur, la température de l’eau aura baissé plus ou moins en sortie pour une même température d’entrée. Plus l’écart sera important, plus le radiateur sera efficace, et inversement. Attention, on ne travaille pas à puissance dissipée constante, mais à écart eau-air constant, c’est différent. Mais n’ayez crainte, par un simple calcul mathématique, nous aurons tout ce dont nous avons besoin par la suite puisqu’il y a une simple relation linéaire qui s’installe. L’équation mise en jeu est la suivante (Equation 1) :
Q = M x Cp x dT
- Q = puissance dissipée par le radiateur en W (à calculer)
- M = débit massique de l’eau en kg/s (mesuré)
- Cp = capacité thermique massique de l’eau en J/kg·K, vaut 4186 J/kg·K ici (connue)
- dT = écart de température entre l’entrée et la sortie du radiateur pour l’eau en K (1 K = 1 °C) (mesuré)
Le deltaT entre l’entrée et la sortie du radiateur dépend de la ventilation et du débit d’eau. Il est toujours très faible, même à haute puissance dissipée, car l’eau a un Cp hors-norme par rapport aux autres liquides. De nombreux points de mesures sont donc pris pour chaque radiateur afin d’avoir le comportement global et non pas un seul point particulier comme de nombreux « tests », car les différences peuvent être importantes.
Cet écart de température d’eau entre l’entrée et la sortie n’est que de quelques degrés tout au plus à très faible débit et pour une grosse puissance à dissiper. Il est de moins de 1 °C en règle générale (débit >2 L/min). Avec cette méthode, il faut disposer d’instruments adaptés permettant une mesure juste à 0.01 °C ou mieux. En effet, le moindre centième de degré équivaut à plusieurs watts après calcul, surtout à haut débit où l’écart entrée-sortie se réduit, ce qui diminue la sensibilité de la mesure :
L’avantage de cette méthode, c’est que l’on connaît exactement la puissance dissipée par chaque radiateur. Il n’y a pas de pertes secondaires indésirables ou de puissances inconnues et variables introduites dans le circuit de mesure (une pompe par ex.). Ici, tout se passe uniquement entre l’entrée et la sortie du radiateur.
La méthode qui consisterait à mesurer l’élévation de température de l’eau par rapport à l’air dans une boucle isolée, où l’on introduirait une puissance de chauffage constante, est l’autre méthode. Elle est valable si l’on prend quelques précautions, car elle introduit des facteurs plus ou moins inconnus, mais elle ne demande pas d’instruments permettant une grande résolution. Chacune des méthodes a ses avantages et inconvénients vis-à-vis de ce que l’on souhaite obtenir et de ce que l’on a à disposition. Soit on travaille à puissance constante pour trouver le deltaT eau-air, soit on travaille à deltaT eau-air constant pour trouver la puissance.







