Résistance de convection
 Voilà la dernière résistance thermique la plus intéressante : celle-ci exprime le fait que la température des parois en contact avec l’eau ne vaut pas la température de l’eau qui circule dans le bloc.
Voilà la dernière résistance thermique la plus intéressante : celle-ci exprime le fait que la température des parois en contact avec l’eau ne vaut pas la température de l’eau qui circule dans le bloc.
Plus on est proche de la paroi plus l’eau est chaude et c’est cette température d’eau près des parois qui va conditionner tout ce qui se trouve en dessous.
On le voit bien sur la photo ci-contre prise par interférométrie différentielle. Elle montre comment la température se répartit autour de 3 tubes. Le fluide chauffé par les tubes voit son indice de réfraction varier, ce qui permet de visualiser la forme du champ de température autour des tubes. On voit bien que les températures ne sont pas du tout homogènes, plus on est proche d’un tube plus le fluide sera chaud. Chaque frange noire représente une plage de température, par exemple le fluide entre 27 et 28 °C. En suivant une même frange, une isotherme, on voit tous les points de l’espace où la température du fluide est entre ces deux températures.
Avant d’aller plus loin dans l’explication, on peut maintenant voir la globalité du phénomène thermique entre l’eau et le core à l’aide de ces 2 schémas de principe.
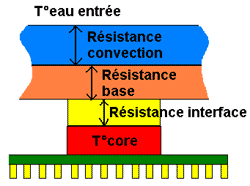
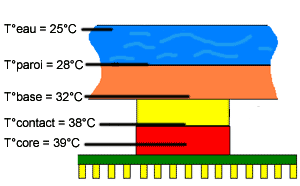
La température du core sera égale à T°core = (Rinterface + Rbase + Rconvection) * Puissance_dissipée + T°eau. La résistance d’interface regroupe la résistance de la pâte due à son épaisseur ainsi que les 2 résistances de contact. La résistance de la base est de manière plus globale la résistance du bloc en lui-même due à la quantité de matière et à sa géométrie. La résistance de convection est la résistance globale du contact eau/paroi sur toute la surface mouillée du bloc. Ces résistances étant par définition en 3D on ne peut pas les calculer à la main, c’est dans ce cas que les simulations numériques viennent à notre secours. Sur le schéma de droite on voit que chaque résistance engendre une hausse de température. Minimiser l’une de ses résistances signifie réduire la température du core et potentiellement augmenter l’overclocking.
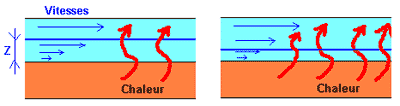
On sait que cette résistance de convection existe car dans n’importe quel écoulement apparaît ce que l’on appelle une couche limite dynamique qui est une sorte de « pellicule » ou « film » d’eau qui colle aux parois. Ce film a une certaine épaisseur qui dépend de la vitesse du fluide près de cette paroi et de la présence ou non de la turbulence. Plus le fluide va lentement plus elle grossit et inversement. Or dans cette couche limite, l’eau qui est très proche de la paroi va se déplacer très lentement à cause des forces de viscosité (vitesse nulle à la paroi), à tel point qu’on la considère comme étant quasiment un solide et donc affublée d’un transfert thermique de type conductif et non plus convectif. Le transfert global n’est alors plus simplement convectif mais conducto-convectif, les 2 modes de transfert se font simultanément.
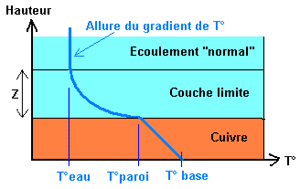
La différence entre conduction et convection est simple. Dans un transfert conductif, il n’y a pas de mouvement de particules à l’échelle macroscopique contrairement à la convection où le fluide est mélangé et brassé. L’eau étant un mauvais conducteur de chaleur, il se forme une sorte de « peau isolante » sur toute la surface mouillée assimilable à une résistance de Fourier. Tout l’intérêt d’un bon bloc est donc de réduire au maximum l’épaisseur de cette couche limite qui existera toujours. Sur le schéma ci-après, Z représente la hauteur de cette couche limite. Plus Z est faible (à droite), plus le transfert de chaleur du cuivre à l’eau est efficace.
Voici maintenant l’allure de l’évolution de la température en fonction des différentes zones traversées. On supposera l’eau à température constante dans l’écoulement normal hors de la couche limite, le vrai profil de température peut varier suivant certains paramètres (nombre de Prandtl). Ce que l’on souhaite réduire par un écoulement adapté c’est la différence T°paroi-T°eau en repoussant le plus près possible l’eau « froide » vers la paroi pour diminuer cet écart :
On sait que cette résistance de convection Rc peut s’exprimer sous la forme Rc = 1/(h*S) avec h le coefficient de convection et S la surface mouillée. On voit que pour diminuer Rc il faut que h*S soit le plus grand possible : il faut donc la surface mouillée la plus importante possible ainsi qu’un h le plus grand possible. Pour la surface rien de compliqué à comprendre, on peut faire l’analogie avec l’aircooling car c’est exactement pareil. Pour h ça se complique un peu car il va dépendre des caractéristiques physiques du fluide, de la géométrie du bloc ainsi que de la forme de l’écoulement qui va imposer une certaine épaisseur à la couche limite (CL). Ce h est régi en partie par l’épaisseur de cette CL, plus celle-ci est fine plus h augmente et inversement. L’idéal est de jouer sur h et S en même temps mais cela s’avère compliqué et on verra que certains blocs très performants jouent beaucoup plus sur h ou sur S.
On va commencer par l’étude et l’influence de la surface dans un bloc. Comme on vient de le dire, plus on a de surface plus on diminue Rc, ça parait simpliste mais il y aura un revers à la médaille. Pour l’augmenter rien de plus facile, il suffit d’usiner de nombreuses ailettes à l’intérieur du bloc al’instar de ces quelques blocs choisis à « multi ailettes » (cliquez pour agrandir) :
Il faut maximiser la surface utile dans le bloc, inutile donc de faire des parcours tortueux qui détruiront le débit à coup sûr pour rien alors qu’il est facile de faire des surfaces droites ou tout en courbe. Par contre, on peut vouloir faire son bloc personnel à design unique avec 36 coudes le long du maze, c’est vous qui choisissez… Pour être efficace une ailette doit être la plus fine possible en général mais le cuivre étant un matériau assez difficile à usiner car il colle aux outils, on est limité à des épaisseurs d’environ 1mm avec une fraiseuse à commande numérique. Il faut le plus de surface mouillée possible à l’intérieur du bloc car sinon à quoi servirait une base de 50 * 50 mm si on ne la remplit pas ou si on ne fait que des canaux uniques très larges. Voici des exemples de ce genre de blocs à canal unique (cliquez pour agrandir) :
Ce qui est dit là est relatif aux moyens d’usinage dont on dispose. Si on ne possède qu’une perceuse sur colonne, il est évident qu’on fera préférentiellement une forme à canal unique. Si on a accès à un centre d’usinage, alors là on peut tout se permettre. Il faut en priorité augmenter la surface vers le centre du bloc, là où on sera le plus chaud. Le genre de blocs en photos ci-dessus nécessitent d’avoir une base moyenne à épaisse pour être le plus efficace possible. C’est ce genre de blocs qui possèdent ce que j’ai appelé un écoulement « basique », rien n’est fait pour accélérer le fluide contrairement aux blocs à impact de jets par exemple. Des bases de 3 à 6 mm d’épaisseur sont recommandées pour obtenir le meilleur de ces blocs.
Une base trop fine ne pourra pas étaler suffisament la chaleur sur les ailettes les plus extérieures, on perd donc de la surface bêtement qui ne servira au final qu’à ralentir le fluide en créant des pertes de charges. Certes on augmentera la Rf de la base à cause de l’épaisseur plus conséquente mais on améliorera de façon sensible la Rc puisque la différence de température entre l’eau et la paroi devient plus faible au fur et à mesure qu’on étale. Le faible h d’un écoulement qui circule dans ce genre de bloc n’a alors plus aucun mal à absorber la puissance. On obtient donc une bonne Rc, une Rf un peu moins bonne mais Rb diminue grâce à Rs qui diminue, donc au final on y gagne partout.
On peut prendre l’exemple du Swiftech MCW5000A qui possède une base épaisse de 6 mm surmontée de pointes de 6 mm de hauteur. La surface offerte à l’eau est très grande de part les nombreuses pointes et la base est suffisamment épaisse pour répartir sur le maximum de pointes. Résultat, il est légèrement mieux qu’un REV3 (graphe C/W) et fait partie des meilleurs blocs à écoulement « basique ». Une version 2 augmente encore ses performances en contraignant le fluide à passer entre les pointes et non plus en partie par le haut. Le couvercle est désormais plat, au ras des pointes et procure une baisse de température supplémentaire de 1.2 °C pour 70 W à 3.8 L/min.







